| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 1149번
- Aimers
- Diffusion
- 일기장
- object detection
- imageclassification
- 객체탐지
- 학습장
- 백준
- pytorch
- 9095번
- 재활용 품목분류
- 다국어 ocr
- 네이버 부스트캠프
- 네이버부스트 캠프
- 타일링2
- 회귀모델
- dp
- 쓰레기분류
- 영수증 ocr
- 네부캠
- 네이버부스트캠프
- 머신러닝 사이클
- 11727번
- zero-shot classification
- 스케치데이터셋
- 스케치이미지
- 부스트캠프
- 모델평가지표
- 코드트리
- Today
- Total
john8538 님의 블로그
[논문 리뷰] Your Diffusion Model is Secretly a Zero-Shot Classifier 본문
https://arxiv.org/abs/2303.16203
대규모 텍스트-이미지 확산 모델이 이미지 생성뿐만 아니라 추가적인 학습 없이 zero-shot classification를 수행가능함을 보여주는 연구
Abstract
- 기존 Diffusion 모델의 한계극복
- 기존에는 이미지 생성에만 집중하였다.
- 그러나 Diffusion 모델의 조건부 밀도 추정을 활용하면 이미지 분류와 같은 다운스트림 작업이 가능하다.
- Diffusion Classifier 제안
- Stable Diffusion 같은 모델을 활용하여 추가적인 학습 없이 zero-shot classification가 가능
- 기존의 지식 추출방법보다 우수한 성과를 보임
- ImageNet에서 학습된 Class-Conditional Diffusion Model을 활용해 학습을 진행하였다.
- 그 결과 기존 모델 대비 Distribution Shift에 대한 강건성(Robustness)이 향상되었다.
Introduction
- Diffusion model의 개요:
확률기반 생성모델로 데이터를 점진적으로 노이즈화(Forward Process)를 한 이후 이를 복원(Backward Process)하는 방식으로 학습을 진행한다. Variational Objective를 사용해여 ELBO(Evidence Lower Bound)를 최적화한다. 일반적으로 Noise Prediction 방식을 사용하여 노이즈를 예측하고 제거하는 과정을 거친다. - Diffusion model을 활용한 이미지 분류:
Diffusion 모델은 조건부 생성 모델이다. 조건부 생성모델은 입력 x와 선택하려는 클래스(유한한 클래스의 집합) c가 주어졌을때 클래스가 주어진 이미지 확률인 pθ(x|c)를 계산가능하다. 이때 베이즈 정리를 적용하면 이미지가 주어졌을 때 클래스의 확률인 $p(c|x)$를 추론할 수 있다.
$p(c \mid x) = \frac{p_{\theta}(x \mid c) p(c)}{p(x)}$
- $pθ(x|c)$: Diffusion 모델을 활용한 클래스 조건부 확률
- $p(c)$: 클래스에 대한 사전 확률 (보통 균등 분포로 가정)
- $p(x)$: 전체 데이터 분포 (정규화 상수)
일반적인 조건부 Diffusion 모델에서는 클래스의 인덱스나 프롬프트를 추가적으로 입력값으로 사용한다.
이때 ELBO를 활용하여 클래스 조건부 로그 확률도 계산이 가능하다.
= 즉 모델이 특정 클래스 c에서 생성한 데이터의 유사도를 추정하는 방식으로 분류가 가능하다.
다시 한번 정리하자면
각 클래스 $c$에 대해, 입력 $x$와의 클래스 조건부 확률 $pθ(x∣c)$을 계산
베이즈 정리를 적용하여 사후 확률 $p(c∣x)$을 추정
클래스 $c$ 중 가장 높은 확률을 가진 클래스를 최종 예측값으로 선택
- Diffusion 모델에서는 분류 확률을 직접 계산하는것은 매우 어렵다. 이때 Monte Carlo 추정을 활용한다. 각 클래스 $c$에 대해 여러 번 샘플링을 수행하고 $ε-prediction loss$(노이즈 복원 오차)를 측정하여 비교한다.
- 이후 오차가 작은 클래스 일수록 더 높은 확률을 할당하는 것이다.
- 이 과정에서 발생하는 분산을 줄이는 전략 뿐만아니라 추론 속도를 최적화하는 기법도 함께 연구하였다.
Figure 1. Overview of our Diffusion Classifier approach

우선 자세히 수식과 설명하기 전에 Figure 1을 보면서 간단하게 전체 패턴을 파악해보자.
Diffusion Classifier는 다음과 같은 과정을 통해 입력 데이터를 분류한다.
- 입력 이미지 $x$ 와 후보 클래스 $c$ 집합이 주어짐
- 예를 들어 Stable Diffusion에서는 후보 클래스가 텍스트 프롬프트가 되고,
- DiT (Diffusion Transformer) 같은 클래스 조건부 Diffusion Model에서는 클래스 인덱스가 후보가 됨.
- 각 클래스 ccc 에 대해 Diffusion Model이 예측한 노이즈 복원 오류(ELBO)를 계산
- Diffusion Model이 특정 클래스 $c$ 를 조건으로 주어진 $x$ 를 얼마나 잘 복원하는지 평가
- 이를 위해 ELBO를 기반으로 $log p_{\theta}(x | c)$ 를 근사함.
- 가장 적합한 클래스 $c^*$ 선택
- 즉 노이즈 복원 오류가 가장 작은 (가장 적합한) 클래스를 선택
- Stable Diffusion의 경우: 가장 적절한 텍스트 프롬프트를 찾음 → Zero-Shot Classification
- DiT (ImageNet Diffusion Transformer) 모델의 경우: 가장 적절한 클래스 인덱스를 찾음 → Supervised Classification
Method
3.1에서는 Diffusion Model의 기본 개념에 대해서 설명을한다.
https://arxiv.org/abs/2006.11239 을 먼저 읽고 온다면 조금 더 이해가 수월할 것이다.
나는 간략하게 이부분을 소개할 예정이다.
Diffusion Model은 Markov Chain 구조를 가지는 생성 모델이다.
- Forward Process:
- 초기 깨끗한 이미지 $X_0$에 점진적으로 가우지안 노이즈를 추가하여 완전한 노이즈인 $X_t$ 형태로 변환하는 과정이다.
- 고정적인 확률 분포를 따르고 학습되지 않는다.
- Reverse Process:
- 학습이 가능한 확률 분포이며 입력에 노이즈가 포함된 상태에서 이를 제거하여 원본 이미지로 복원하는 역할을 가진다.
- 특정 조건 $c$(아까말했던 클래스 인덱스나 텍스트 프롬프트)를 입력받아 이를 기반으로 복원한다
Diffusion Model이 특정 조건 $c$ 를 기반으로 원본 이미지를 생성할 확률 $pθ(x0|c)$를 추정할 수 있다면 이를 이용해 분류 문제를 해결할 수도 있음.
이 확률을 직접 계산하는 것은 매우 어렵기 때문에 ELBO(Evidence Lower Bound) 근사를 활용하여 최적화함.
3.2 에서는 Diffusion 모델을 이용한 분류에 대해 조금더 자세히 공식을 활용하여 설명한다.
아이디어 1. 베이즈 정리를 활용한 분류 가능성 계산
- 일반적인 생성 모델을 이용한 분류는 아래와 같은 베이즈 공식을 활용하여 수행한다.
$p_{\theta}(c_i | x) = \frac{p(c_i) p_{\theta}(x | c_i)}{\sum_{j} p(c_j) p_{\theta}(x | c_j)}$
모델 예측과 레이블에 대한 c클래스의 확률(prior p(c)) 베이즈 정리 - 만약 사전확률 $p(ci)$이 균등 분포라면 분모의 모든 $p(c)$가 상쇄되어 단순한 형태로 변형이 된다.
아이디어 2. Diffusion Model을 사용한 분류
- 기존 생성 모델과 다르게 Diffusion Model에서는 $pθ(x0|c)$를 직접 계산하는 것이 비현실적이다. (계산이 어렵고 계산량이 많기 때문)
- 이를 ELBO를 활용하여 근사적으로 분류 가능성을 계산한다.

즉 입력 이미지 x에 대해 각 클래스 c를 조건으로 주었을 때 Diffusion Model이 얼마나 정확하게 노이즈를 복원할 수 있는지를 기반으로 분류한다.
Monte Carlo 추정 (Sampling 기반 계산)
- 기대값 $\mathbb{E}_{t, \varepsilon}$ 를 직접 계산하는 것은 어렵기 때문에 Monte Carlo 방법을 활용함.
- 랜덤 샘플링된 $t$ 와 $ε$에 대해 반복적으로 평가하여 확률을 근사함.
이 방법의 장점:
- 기존의 Diffusion Model을 그대로 활용 가능 → 추가적인 학습 없이 Zero-Shot 분류 가능!
- Stable Diffusion 같은 Text-to-Image 모델에서도 활용 가능 (Zero-Shot Text Classification)
- DiT 같은 클래스 조건부 모델에서는 기존 분류기처럼 활용 가능 (Supervised Classification)
3.3 에서는 분산 감소 기법에 대해 설명한다.
현재의 문제점은 Monte Carlo 방법을 사용하려면 기대값을 근사해야하는데 이를 위해서는 수천 개의 샘플이 필요할 수 있다는 점이다. 계산 비용이 크고 샘플 변동성(Variance)이 너무 커서 안정적인 분류가 어려울 수 있다.
이를 해결하기 위해 Difference Testing 기법을 도입한다.
- 기존에는 각 클래스에 대해 독립적으로 샘플을 생성하여 비교했다.
- 그러나 절대적인 오류 크기가 아니라 클래스 간의 상대적인 오류차이만 필요하다.
- 고정된 샘플 집합 $S = \{ (t_i, \varepsilon_i) \}_{i=1}^{N}$ 을 사용하여 모든 클래스 c 에 대해 동일한 샘플을 평가
- 즉 c 가 바뀌어도 같은 노이즈 샘플 ε 과 타임스텝 t 를 사용하여 평가하면, 개별 샘플의 변동성(Variance)을 줄일 수 있음.
결과적으로 통계적 검정과 유사한 원리로 분산을 줄였다.
같은 샘플을 비교하므로 차이를 더 정확하게 측정할 수 있으며 실험결과 적은 샘플 수로도 분류가 가능해졌다.
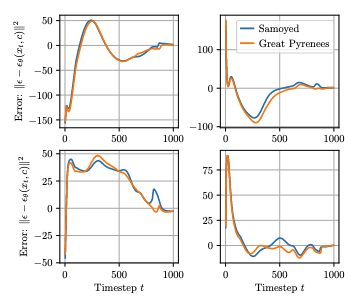
그림 2는 이 아이디어를 시각화한 예시로 "Samoyed"와 "Great Pyrenees"라는 두 가지 프롬프트에 대해Great Pyrenees 이미지를 사용하여 ϵ-예측 오류를 보여준니다. 각 서브플롯은 하나의 ϵi에 해당하며, 오류는 $t∈{1,2,…,1000}$ 에서 평가된다.
주목할 점은 서로 다른 ϵi 샘플에 대한 ϵ-예측 오류의 분산이 상당히 크지만, 두 프롬프트 간 오류 차이의 분산은 훨씬 더 작다는 것이다. 이는 예측 오류의 차이가 클래스 간 구분을 위해 더 일관되고 신뢰할 수 있음을 나타낸다. 따라서 모든 조건부 입력에 대해 동일한 $(ti,ϵi)$를 사용함으로써 $p_{\theta}(c_i | x)$의 추정이 훨씬 더 정확해진다.
Practical Considerations
Diffusion Classifier는 이미지를 분류하기 위해 각 클래스마다 반복적인 오류 예측 평가가 필요하다. 이러한 평가는 3.3절에서 제시된 방법을 사용하더라도 상당한 추론 시간이 소요된다. 이 절에서는 추론 시간을 단축할 수 있는 추가적인 통찰과 최적화 방법들을 제시하고 있다.
1. 시간 단계의 효과 (Effect of timestep)
Diffusion Classifier는 $p_{\theta}(c_i | x)$를 추정하기 위해 시간 단계 $t$에 대해 균일 분포를 사용하여 ε-예측 오류를 추정한. 다른 시간 분포를 사용하면 더 정확한 결과를 얻을 수 있는지 확인한다.

그림 3은 각 클래스마다 단일 시간 단계만을 평가하여 Pets 데이터셋에 대한 정확도를 보여주는데, 직관적으로 정확도는 중간 시간 단계 t≈500일 때 가장 높다.
이는 다음과 같은 질문을 제기한다: 중간 시간 단계를 과샘플링하고, 낮거나 높은 시간 단계를 저샘플링함으로써 정확도를 개선할 수 있을까? 이에 저자는 여러 가지 시간 단계 샘플링 전략을 시도한다:

그림 4는 다양한 전략에서 샘플을 더 많이 사용할 때 평균 오류가 개선됨을 보여준다. 특히 균등 간격 시간 단계를 사용하는 것이 가장 효과적임을 확인할 수 있다. 또한 소수의 $t_i$를 반복적으로 사용하는 것이 ELBO 추정에 편향을 줄 수 있기 때문에 효율성이 떨어진다고 가설을 세운다.
2. 효율적인 분류 (Efficient Classification)
평가를 여러 단계로 나누어 각 단계에서 남아있는 클래스들을 일정 횟수만큼 시도하고 가장 큰 평균 오류를 보이는 클래스를 제외하는 방식으로 최적화를 진행하였다. 이 방법은 최종 출력이 아닌 클래스를 효율적으로 제거하고, 합리적인 클래스들에 대해 더 많은 계산을 할당할 수 있게 해준다.
예를 들어, Pets 데이터셋에서는 Nstages = 2로 설정하여 첫 번째 단계에서는 각 클래스를 25번 시도하고 평균 오류가 작은 5개의 클래스를 선택한다. 두 번째 단계에서는 남은 5개의 클래스에 대해 225번을 추가로 시도다. 이 방식으로 분류하는 데 걸리는 시간은 RTX 3090 GPU에서 18초로 확인되었다.
이러한 평가 전략을 통해 이미지넷과 같이 1000개 클래스가 있는 경우에도 적응형 전략을 사용하더라도 분류 시간이 약 1000초에 이르는 문제가 있지만 더 빠른 추론 시간을 위한 향후 연구가 필요하다고 말한다.


- 주요 결과: Diffusion Classifier는 추가적인 학습이나 레이블 없이도 Synthetic SD Data와 같은 대체 제로샷 접근 방식과 SD Features(전체 레이블된 학습 데이터를 사용한 감독 학습된 분류기)를 초과하는 성능을 보인다.
- 비교: Diffusion Classifier는 CLIP ResNet-50과 OpenCLIP ViT-H와 경쟁할 만큼 뛰어난 성능을 보였으며 이는 생성적 모델에서 큰 발전을 나타낸다.
- 핵심: Stable Diffusion의 훈련 데이터셋이 더 다양하게 확장된다면 성능이 더 향상될 가능성이 있습니다. (예: LAION-5B보다 덜 선별된 데이터셋으로 훈련)
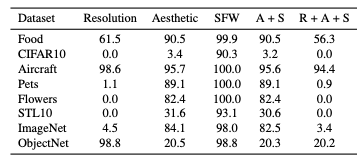

- Winoground 벤치마크: Diffusion Classifier는 CLIP과 같은 대비 모델에 비해 객체 및 관계 교환 작업과 같은 구성적 추론 과제에서 현저히 우수한 성능을 보인다.
- 핵심: Diffusion Classifier는 더 나은 교차 모달 결합을 통해 구성적 추론 능력이 뛰어난 성능을 보였고Stable Diffusion이 훈련 없이도 강력한 분류기와 추론기로 변환될 수 있음을 보여준다.

- 비교: Diffusion Classifier는 ImageNet에서 훈련된 ViT와 ResNet 모델들과 비교했을 때, 성능 면에서 우위를 점한다.
- 핵심: Diffusion Classifier는 256² 해상도에서 77.5%, 512² 해상도에서 79.1%의 정확도를 기록하며, 생성 모델이 분류 성능에서도 우수하다는 점을 보인다.
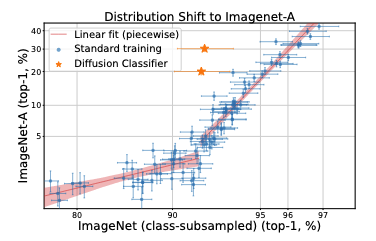
- 주요 결과: Diffusion Classifier는 고급 데이터 증강 기법 없이도 안정적인 훈련이 가능하며 과적합을 방지하면서 높은 정확도를 기록했다.
- 핵심: ViT 훈련의 불안정성과 비교했을 때 Diffusion Classifier는 학습 안정성에서 큰 장점을 보인다.
Conclusion
- 제로샷 및 표준 분류 성능: Diffusion Classifier는 제로샷 및 표준 분류에서 최신 discriminative 방법들과의 격차를 줄였으며 멀티모달 구성 추론에서는 이들을 상당히 능가하는 성능을 보였다.
- 배포 변화에 대한 강력한 성능: Diffusion Classifier는 배포 변화(Distribution Shift)에 대해서도 기존 모델들보다 뛰어난 효과적인 강건성을 나타냈다.
